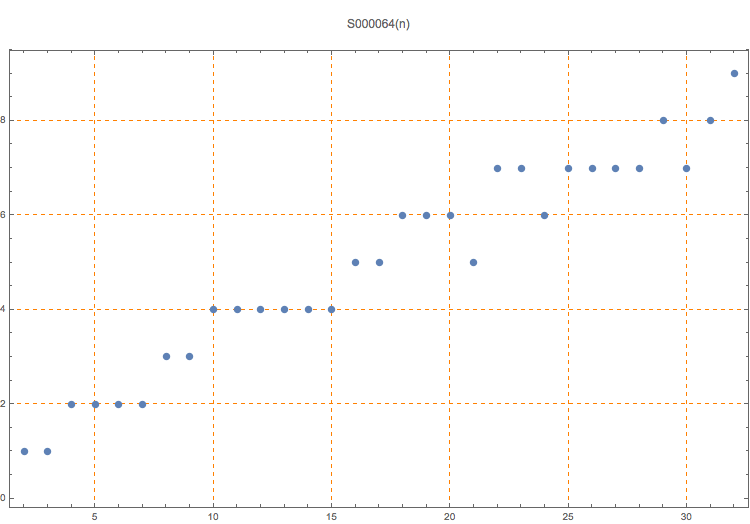
Conjectured maximum number of primes between n*k and n*(k+1) for some k > 0.
1, 1, 2, 2, 2, 2, 3, 3, 4, 4, 4, 4, 4, 4, 5, 5, 6, 6, 6, 5, 7, 7, 6, 7, 7, 7, 7, 8, 7, 8, 9
2
Primes less than 2*10^9 were used to check these values. The conjectured value of k is given in S000065. Note that we exclude the endpoints n*k and n*(k+1). The offsets are given in S000066. The section in the book by Guy covers similar subjects.
The term s(32) was corrected to 9 by Emmanuel Vantiegheim, Jan 10 2016.
T. D. Noe, Plot of terms 2 to 32
Richard K. Guy, Unsolved Problems in Number Theory, Springer, Third Edition, 2004, A9.
Examples:
For n = 2, there can be only one prime: all odd primes satisfy.
For n = 3, there can be only one prime: 3k+2 for odd k and 3k+1 for even k.
For n = 4, there can be up to 2 primes: 4k+1 and 4k+3.
(Mma) Table[mx = {}; Do[s = Select[n*i + Range[n], PrimeQ]; If[Length[s] > Length[mx], mx = s - n*i], {i, 10^7}]; Length[mx], {n, 2, 31}]
nonn,hard,nice
T. D. Noe, May 29 2014