Table of initial primes such that there are k consecutive primes that are equal (mod n), with k > 1 and n > 2.
23, 47, 7, 251, 89, 139, 1741, 199, 1627, 23, 1741, 463, 18839, 47, 113, 19471, 463, 123229, 251, 5939, 89, 118801, 463, 776257, 1741, 158867, 1823, 523, 148531, 11593, 3873011, 1741, 894287, 20809, 15823, 139, 148531, 11593, 23884639, 19471, 6996307
1
The triangle is read by antidiagonals. See theorem 1.2 (Shiu) in the paper by Pan and Sun.
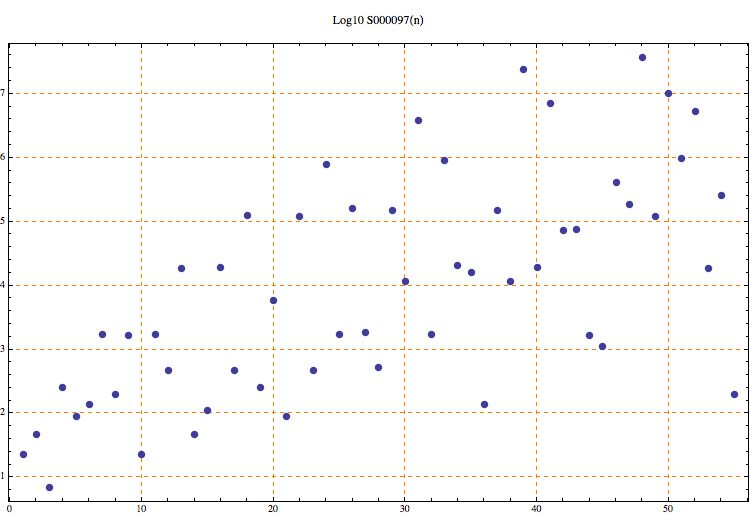
T. D. Noe, Plot of first 10 rows
T. D. Noe, Table of first 10 rows
Hao Pan and Zhi-Wei Sun, Consecutive primes and Legendre symbols, arXiv 1406.5951, Jun 23 2014.
D. K. L. Shiu, Strings of congruent primes, J. London Math. Soc. 61 (2000), 359–373.
Example, rows:
23, 47, 251, 1741, 1741, 19471, 118801, 148531, 148531, 406951, 1820111, 2339041,…
7, 89, 199, 463, 463, 463, 11593, 11593, 183091, 241603, 241603, 241603, 9177431, 9177431,…
139, 1627, 18839, 123229, 776257, 3873011,…
23, 47, 251, 1741, 1741, 19471, 118801, 148531, 148531, 406951, 1820111, 2339041,…
113, 5939, 158867, 894287, 6996307, 9984437,…
89, 1823, 20809, 73133, 989647, 3250469, 9065867,…
523, 15823, 74453, 5321191, 5379113,…
139, 1627, 18839, 123229, 776257, 3873011,…
1129, 259033, 1736281,…
199, 199, 12829, 180799, 180799, 1248869, 7790917,...
(Mma) lim = 12; t2 = {}; Do[t = {}; lastM = 0; firstP = 0; cnt = 0; mx = 1; n = 0; While[Length[t] < lim - k + 1, n++; p = Prime[n]; m = Mod[p, k]; If[m == lastM, cnt++; If[cnt > mx, mx = cnt; AppendTo[t, firstP]], cnt = 1; lastM = m; firstP = p]]; Print[t]; AppendTo[t2, t], {k, 3, lim}]; Flatten[Table[t2[[i, n - i + 1]], {n, lim - 2}, {i, n}]]
Cf. A054679, A054678, A054681 (first three rows in the example section).
nonn,tabl,hard
T. D. Noe, Jun 24 2014