Primitive Pythagorean triples (a, b, c^3) for prime c.
44, 117, 125, 828, 2035, 2197, 495, 4888, 4913, 15939, 18460, 24389, 27755, 42372, 50653, 42471, 54280, 68921, 14715, 148148, 148877, 117469, 194220, 226981, 213785, 325008, 389017, 146960, 689481, 704969, 539352, 736255, 912673, 580060, 851499, 1030301
1
Of course, c mod 4 == 1. Cheng and Gordon show that these triangles have angles that can be trisected. When c is composite, it is possible for there to be multiple triangles that have hypotenuse c^3; when c is prime, there is only one such triangle. More general c is treated in S000186.
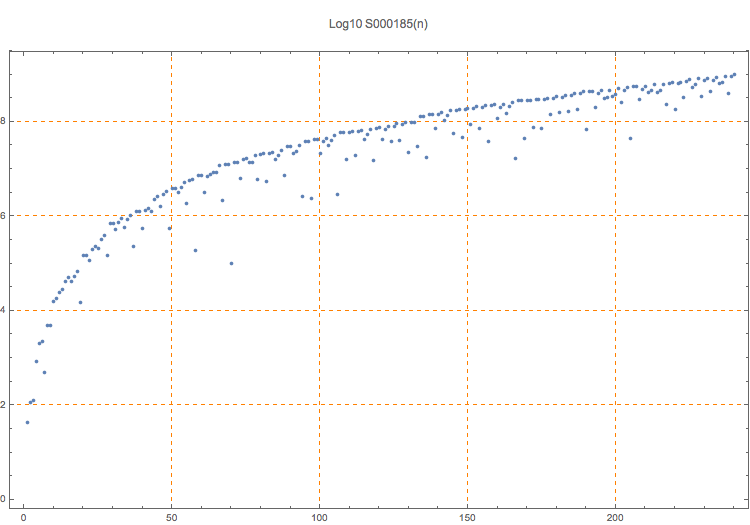
T. D. Noe, Plot of 80 triples (for c < 1000)
T. D. Noe, Table of 80 triples (for c < 1000)
Wen D. Cheng and Russell A. Gordon, Trisecting angles in Pythagorean triangles, Amer. Math. Monthly, 121 (2014), pp. 625-631.
(Mma) t = {}; Do[If[Mod[p, 4] == 1, c = p^3; a = 0; While[a++; b = Sqrt[c^2 - a^2]; 2*a^2 < c^2 && (! IntegerQ[b] || GCD[a, b] > 1)]; AppendTo[t, {a, b, c}]], {p, Prime[Range[26]]}]
Cf. A103606 (primitive Pythagorean triples).
nonn,tabl
T. D. Noe, Aug 07 2014