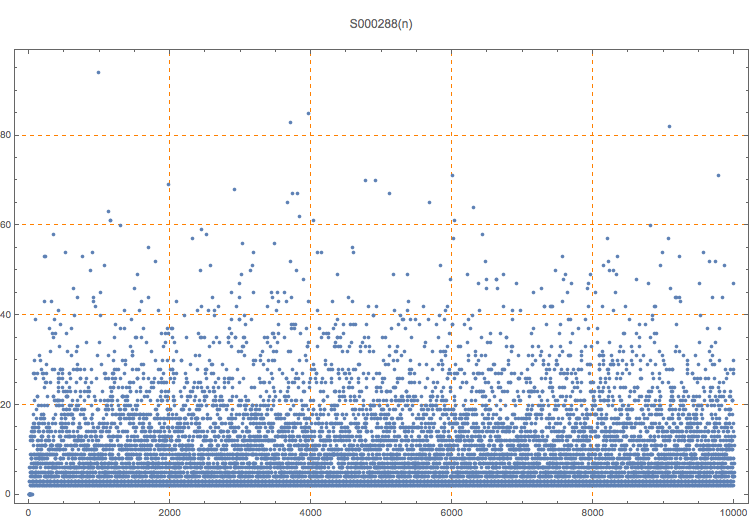
Position of first zero digit in 4^n, counting from the right.
0, 0, 0, 0, 0, 3, 3, 0, 0, 0, 6, 2, 0, 5, 0, 9, 0, 0, 0, 5, 12, 2, 6, 13, 4, 8, 4, 8, 9, 13, 8, 2, 8, 5, 14, 5, 0, 7, 0, 14, 5, 2, 12, 0, 3, 13, 12, 15, 4, 5, 5, 2, 3, 3, 7, 3, 3, 4, 18, 6, 7, 2, 16, 6, 14, 9, 11, 27, 14, 4, 13, 2, 4, 9, 9, 27, 7, 30, 21, 16, 15
0
Zero indicates that there are no zeros in the number. Is there a maximum value for this function? This question was discussed in MathOverflow. The number a(n) is the same as S000286(2n).
T. D. Noe, Plot of 10001 terms
T. D. Noe, Table of 10001 terms
MathOverflow, Zeros in the representation of powers of 3
(Mma) Table[s = Position[Reverse[IntegerDigits[4^n]], 0]; If[Length[s] == 0, 0, s[[1, 1]]], {n, 0, 100}]
nonn,base
T. D. Noe, Oct 12 2014