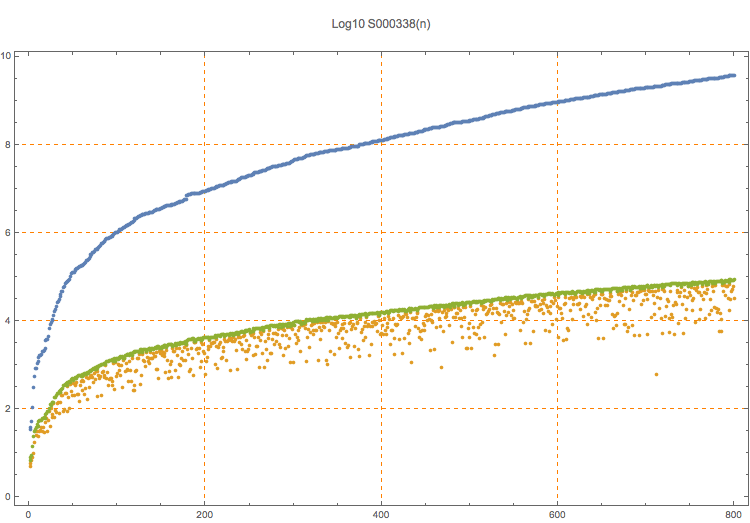
Three sides of right triangles having legs that are triangular numbers, ordered by hypotenuse.
35, 6, 7, 39, 5, 8, 53, 7, 9, 111, 8, 14, 305, 10, 24, 555, 18, 32, 822, 32, 35, 845, 25, 39, 1122, 32, 44, 1189, 40, 41, 1515, 24, 54, 1628, 32, 55, 1639, 33, 55, 1709, 38, 55, 2015, 31, 62, 2103, 39, 62, 2125, 29, 64, 2359, 49, 63, 3653, 64, 77, 3816, 63, 80
1
Let tri(n) be the n-th triangular number n*(n+1)/2. The order of the three numbers is: hypotenuse, x, and y, where tri(x) is the short side, and tri(y) is the long side. The three numbers are shown in different colors in the plot above.
T. D. Noe, Plot of 800 triples
T. D. Noe, Table of 800 triples
Ricardo Buring, MathOverflow: How many Pythagorean triples are there in which every member is triangular?
Maciej Ulas, On certain diophantine equations related to triangular and tetrahedral numbers, arXiv 0811.2477 (Nov 15 2008)
Eric W. Weisstein, MathWorld: Triangular Number
The first term, 35, is the hypotenuse of the right triangle whose sides are 21 and 28, the sixth and seventh triangular numbers.
(Mma) nn = 1000; t = {}; mx = 1 + (1/4) nn^2 (nn + 1)^2; Do[z2 = (a^2 (a + 1)^2 + b^2 (b + 1)^2)/4; If[z2 <= mx && IntegerQ[z = Sqrt[z2]], AppendTo[t, {z, a, b}]], {a, nn}, {b, a, nn}]; t = Sort[t]
Cf. S000337 (hypotenuses), S000339, S000340.
nonn,nice
T. D. Noe, Nov 13 2014, extended Nov 18 2015