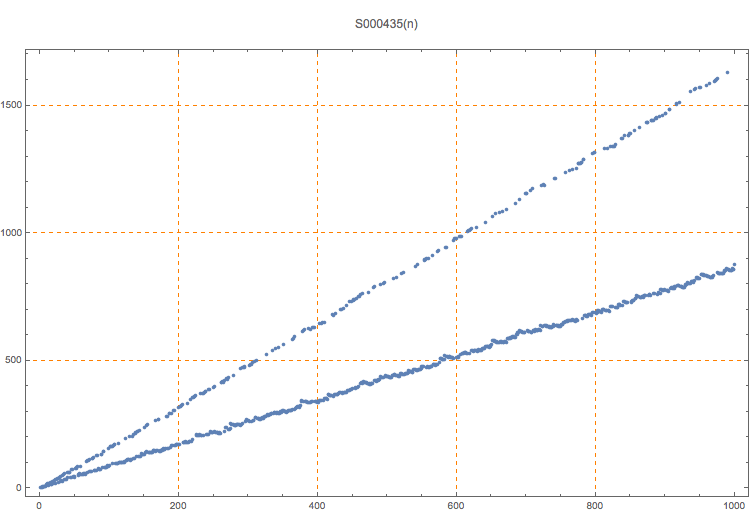
Conjectured number of terms required for the conductor function in S000434 to converge.
2, 3, 4, 6, 7, 8, 7, 6, 14, 10, 18, 19, 12, 13, 24, 15, 16, 28, 18, 28, 31, 20, 36, 36, 38, 24, 38, 41, 26, 45, 29, 28, 50, 53, 33, 57, 35, 34, 61, 42, 61, 61, 63, 40, 40, 73, 74, 44, 43, 44, 79, 78, 82, 85, 52, 51, 56, 87, 54, 53, 52, 54, 57, 56, 55, 56, 105, 60
1
Note that there appear to be two sets of primes. These are shown in S000436 and S000437. See the Bessoud and Wagon book for more information about the conductor (but not this function).
T. D. Noe, Plot of 1000 terms
T. D. Noe, Table of 1000 terms
David Bessoud and Stan Wagon, A Course in Computational Number Theory, Key College Publishing, 2000.
(Mma) Needs["CNT`”]; nn = 50; v = Table[p = Prime[Range[n, 4*n]]; Conductor[p], {n, nn}]; Table[i = 2; While[p = Prime[Range[n, n + i - 1]]; Conductor[p] > v[[n]], i++]; i, {n, nn}]
Cf. S000434, S000436, S000437.
nonn,nice
T. D. Noe, Dec 27 2014