Primitive Pythagorean triples in which the two legs are palindromes.
3, 4, 5, 464, 777, 905, 313, 48984, 48985, 34743, 42824, 55145, 25652, 55755, 61373, 52625, 80808, 96433, 575575, 2152512, 2228137, 80308, 5578755, 5579333, 2532352, 5853585, 6377873, 5679765, 23711732, 24382493, 304070403, 402080204, 504110405
1
The triples are shown sorted: x, y, z with x^2 + y^2 = z^2. The numbers 464 and 777 are the palindromic legs of the second triple.
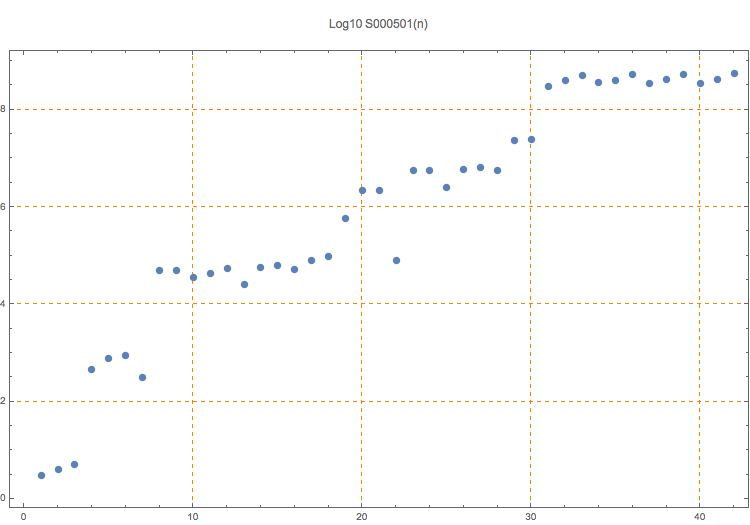
T. D. Noe, Plot of 14 triples
T. D. Noe, Table of 14 triples
J. R. Antalan, StackExchange: A tale of two palindromes (sum of squares of two palindromes is a perfect square)
John Rafael M. Antalan and Richard P. Tagle, Numeric palindromes in primitive and non-primitive Pythagorean triples, arxiv.org 1502.06760 (Feb 24 2015)
Eric W. Weisstein, MathWorld: Pythagorean Triple
(Mma) nn = 999; PerfectSquareQ[n_] := JacobiSymbol[n, 13] =!= -1 && JacobiSymbol[n, 19] =!= -1 && JacobiSymbol[n, 17] =!= -1 && JacobiSymbol[n, 23] =!= -1 && IntegerQ[Sqrt[n]]; pal = Table[s = IntegerDigits[n]; {FromDigits[Join[Most[s], Reverse[s]]], FromDigits[Join[s, Reverse[s]]]}, {n, nn}]; pal = Sort[Flatten[pal]]; t = {}; Do[If[x < y && GCD[x, y] == 1 && PerfectSquareQ[x^2 + y^2], z = Sqrt[x^2 + y^2]; If[z <= pal[[-1]], AppendTo[t, {x, y, z}]]], {x, pal}, {y, pal}]; Sort[t, #1[[3]] < #2[[3]] &]
Cf. S000502-S000509, S000579, S000580.
nonn,base,hard,nice
T. D. Noe, Feb 25 2015