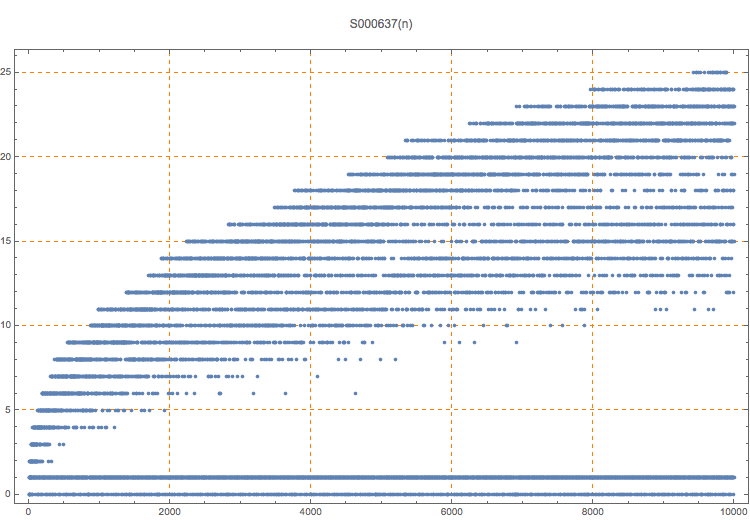
The number of ways number n can be written as the sum of a squarefree number and a prime squared.
0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 2, 1, 0, 2, 2, 1, 1, 1, 2, 1, 1, 1, 2, 1, 1, 2, 2, 2, 0, 3, 2, 2, 1, 1, 3, 1, 1, 3, 3, 2, 1, 3, 2, 2, 1, 3, 3, 2, 0, 2, 4, 2, 0, 2, 4, 3, 1, 1, 3, 3, 1, 4, 3, 3, 1, 4, 2, 3, 1, 3, 4, 2, 1, 2, 3, 2, 1, 4, 2, 3, 1, 4, 4, 2, 0, 4, 4
1
Dudek and Platt prove that every number n >= 10 with n =/= 1 mod 4 can be written as the sum of a prime squared and a squarefree number. See S000638 for the numbers not representable.
T. D. Noe, Plot of 10000 terms
T. D. Noe, Table of 10000 terms
Adrian Dudek and David J. Platt, On a theorem of Erdos in additive number theory, arXiv 1510.03677 (Apr 14 2015)
(Mma) nn = 100; sqFree = Select[Range[nn], SquareFreeQ]; prime2 = Prime[Range[PrimePi[Sqrt[nn]]]]^2; ta = Tally[Sort[Select[Flatten[Table[a + b, {a, sqFree}, {b, prime2}]], # <= nn &]]]; tb = Complement[Range[nn - 1], Transpose[ta][[1]]]; tc = Transpose[{tb, Table[0, {Length[tb]}]}]; Transpose[Union[ta, tc]][[2]]
Cf. S000638.
nonn
T. D. Noe, May 15 2015