Irregular table of difference equations and initial terms descibed in S000642.
7, -7, 1, 0, 3, 20, 7, -7, 1, 0, 6, 40, 7, -7, 1, 0, 9, 60, 7, -7, 1, 0, 12, 80, 7, -7, 1, 0, 15, 100, 7, -7, 1, 0, 18, 120, 1, 0, 6, -6, 0, -1, 1, 0, 5, 8, 21, 48, 65, 140, 7, -7, 1, 0, 24, 160, 7, -7, 1, 0, 27, 180, 7, -7, 1, 0, 30, 200, 7, -7, 1, 0, 33, 220
1
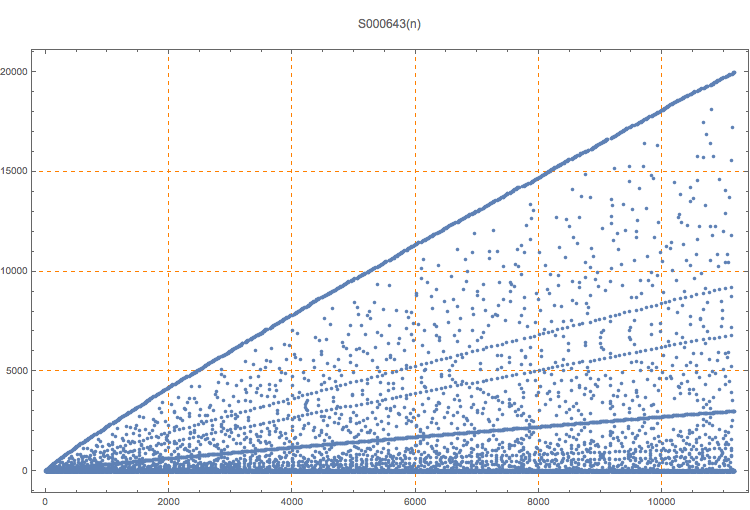
Row n has 2*S000642(n) terms. Note that the first term of the initial terms is always 0. The initial terms of the third-order difference equations are (0, 3*n, 20*n). These correspond to the heavy lines in the graph above. The higher-order difference equations appear to be more complicated. See S000648.
T. D. Noe, Plot of 1000 rows
T. D. Noe, Table of 1000 rows
(Mma) PerfectSquareQ[n_] := JacobiSymbol[n, 13] =!= -1 && JacobiSymbol[n, 19] =!= -1 && JacobiSymbol[n, 17] =!= -1 && JacobiSymbol[n, 23] =!= -1 && IntegerQ[Sqrt[n]]; FindCoef[seq_List, i_, n_] := Module[{m, a, s, noSoln = {}}, a = Take[seq, {i, i + 2 n - 1}]; m = Reverse /@ Partition[Most[a], n, 1]; If[Det[m] == 0, noSoln, s = LinearSolve[m, Take[a, -n]]; If[And @@ IntegerQ /@ s, s, noSoln]]]; Table[td = {}; n = 0; c = {}; While[If[PerfectSquareQ[n^2 + (n + d)^2], AppendTo[td, n]; If[Length[td] > 2 && OddQ[Length[td]], c = FindCoef[td, 1, (Length[td] - 1)/2]]]; c == {}, n++]; {c, Take[td, Length[c]]}, {d, 20}]
sign,tabf,hard,nice
T. D. Noe, May 21 2015