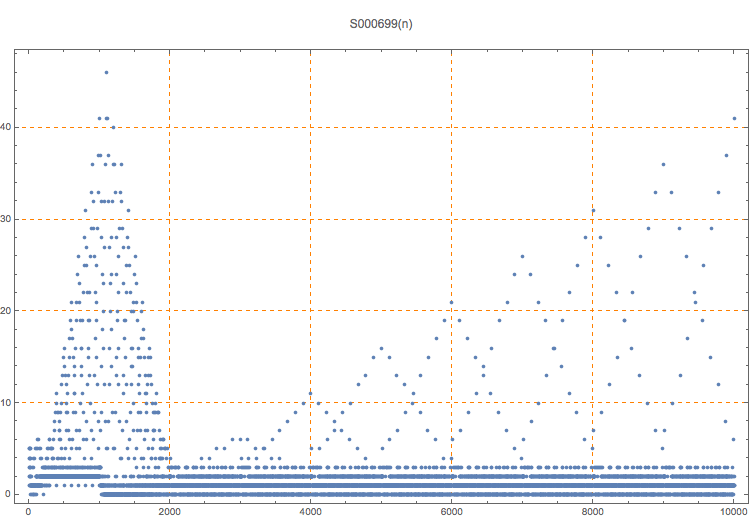
Number of palindromic pairs that sum to n.
1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 5, 5, 5, 4, 4, 3, 3, 2, 2, 1, 1, 0, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 3, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 3, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 4, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 4, 1, 1, 1, 1, 1, 1, 1, 1, 1
0
Note that there are many zero terms. Compare S000698. This is the same as A260254.
T. D. Noe, Plot of 10000 terms
T. D. Noe, Table of 10000 terms
T. D. Noe, Plot of 200000 terms
William D. Banks, Every natural number is the sum of forty-nine palindromes, arXiv 1508.04721 (Aug 19 2015)
(Mma) palindrome[b_Integer, n_Integer, del_] := Module[{c = IntegerDigits[n, b], d}, d = If[del, Join[c, Reverse[Most[c]]], Join[c, Reverse[c]]]; FromDigits[d, b]]; tp1 = Table[palindrome[10, n, True], {n, 99}]; tp2 = Table[palindrome[10, n, False], {n, 99}]; tp3 = Union[{0}, tp1, tp2]; tt = Tally[Sort[Flatten[Table[tp3[[a]] + tp3[[b]], {a, Length[tp3]}, {b, a, Length[tp3]}]]]]; tn = Complement[Range[0, tp3[[-1]] + 1], Transpose[tt][[1]]]; Transpose[Take[Union[tt, Transpose[{tn, Table[0, {Length[tn]}]}]], tp3[[-1]] + 1]][[2]]
Cf. A002113 (palindromes in base 10), A260254, S000698-S000708.
nonn,base
T. D. Noe, Aug 26 2015