Triples of nonnegative (a,b,c) such that a*b-c, b*c-a, and c*a-b are all powers of 2.
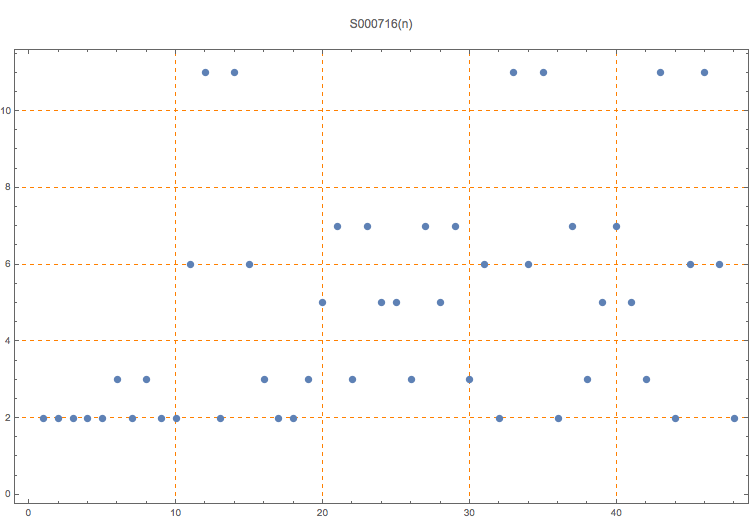
2, 2, 2, 2, 2, 3, 2, 3, 2, 2, 6, 11, 2, 11, 6, 3, 2, 2, 3, 5, 7, 3, 7, 5, 5, 3, 7, 5, 7, 3, 6, 2, 11, 6, 11, 2, 7, 3, 5, 7, 5, 3, 11, 2, 6, 11, 6, 2
1
There are essentially only four solutions: (2,2,2), (2,2,3), (2,6,11), and (3,5,7). With permutations, they become the 16 solutions shown here.
T. D. Noe, Plot of 16 triples
IMO, 2015 Results (see problem 2)
Victor Pambuccian, A problem in Pythagorean Arithmetic, arXiv 1510.01645 (Oct 04, 2015)
(Mma) nn = 20; t = {}; Do[If[IntegerQ[Log[2, a*b - c]] && IntegerQ[Log[2, b*c - a]] && IntegerQ[Log[2, c*a - b]], AppendTo[t, {a, b, c}]], {a, 0, nn}, {b, 0, nn}, {c, 0, nn}]; Flatten[t]
nonn,full
T. D. Noe, Oct 06 2015