Least Hamming weight of a multiple of prime(n).
1, 2, 2, 3, 2, 2, 2, 2, 3, 2, 5, 2, 2, 2, 3, 2, 2, 2, 2, 3, 3, 3, 2, 4, 2, 2, 3, 2, 2, 2, 7, 2, 2, 2, 2, 3, 2, 2, 3, 2, 2, 2, 3, 2, 2, 3, 2, 4, 2, 2, 4, 3, 2, 2, 2, 3, 2, 3, 2, 2, 2, 2, 2, 3, 2, 2, 2, 3, 2, 2, 2, 3, 3, 2, 2, 3, 2, 2, 2, 2, 2, 2, 4, 2, 3, 2, 2
1
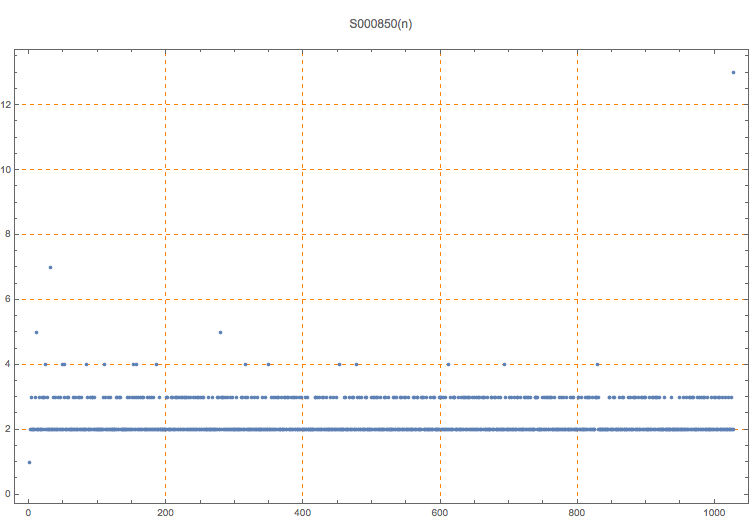
The Hamming weight of an integer is the number of 1’s in binary. For example, the Hamming weight of 23 is 4 because 23 = 10111 in base 2. It appears that almost all primes have a least Hamming weight less than 5. The least multiple of prime(n) having the lowest Hamming weight can be quite large; see S000851. This topic is related to sturdy numbers; see A143027 and S000848.
T. D. Noe, Plot of 1028 terms (for primes up to 8191)
T. D. Noe, Table of 1028 terms (for primes up to 8191)
Christian Elsholtz, Almost all primes have a multiple of small Hamming weight, arXiv 1602.05974 (Feb 18 2016)
T. D. Noe, Mathematica program for computing this sequence
Cf. A143027, S000848, S000851.
nonn,base,nice
T. D. Noe, Feb 24 2016