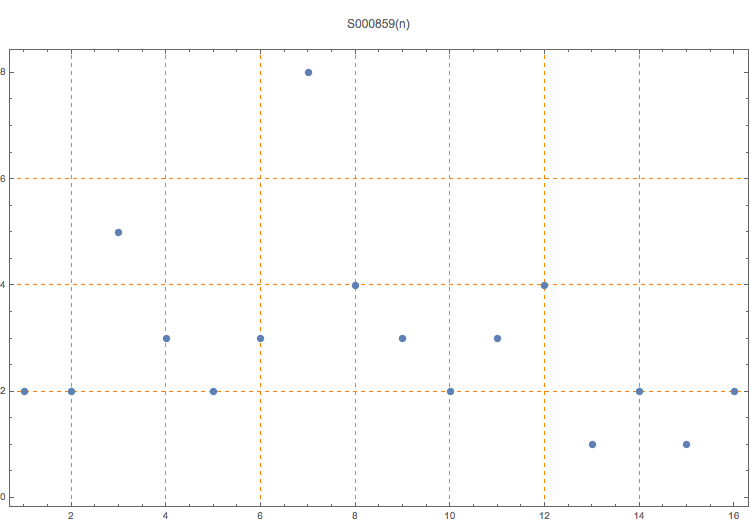
Number of numbers having n digits chosen from 1, 3, 7, and 9 containing S000857(n) primes.
2, 2, 5, 3, 2, 3, 8, 4, 3, 2, 3, 4, 1, 2, 1, 2
1
It is somewaht surprizing to see that there are so few numbers having the maximum number of primes. This fact makes it unlikely that a random choice of digits will be optimal.
After computing all 4^15 and 4^16 numbers, added 1 and 2. - T. D. Noe, May 02 2016
T. D. Noe, Plot of 16 terms
Carlos B. Rivera, Prime Puzzle 823: String of digits 1379 full of primes
(Mma) digits = {1, 3, 7, 9}; t = Table[mx = 0; cnt = 0; Do[d = digits[[IntegerDigits[i, 4, numLen] + 1]]; t2 = Union[Flatten[Table[FromDigits[Take[d, {i, j}]], {i, numLen}, {j, i, numLen}]]]; len = Length[Union[Select[t2, PrimeQ]]]; If[len == mx, cnt++, If[len > mx, mx = len; cnt = 1; dBest = FromDigits[d]]], {i, 0, 4^numLen - 1}]; Print[{numLen, mx, dBest, cnt}]; {mx, dBest, cnt}, {numLen, 10}]; Transpose[t][[3]]
nonn,base,hard,more
T. D. Noe, Mar 29 2016