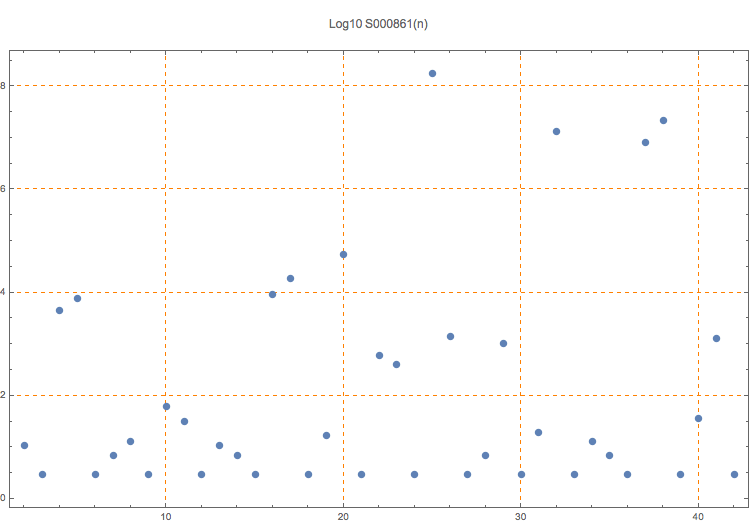
Least prime dividing RNL(n) = sum(k=1..n) 10^(n!-k!).
11, 3, 4447, 7823, 3, 7, 13, 3, 61, 31, 3, 11, 7, 3, 9281, 19163, 3, 17, 53861, 3, 599, 397, 3, 174443251, 1423, 3, 7, 1019, 3, 19, 13086683, 3, 13, 7, 3, 8157599, 21777149, 3, 37, 1291, 3
2
It appears that 11 is the only known prime in the RNL function. The first missing term here is for RNL(25), which is larger that the largest known prime.
T. D. Noe, Plot of terms 2..42
Carlos B. Rivera, Prime Puzzle 825: Primes of type Liouville
(Mma) Table[p = 3; While[Mod[Sum[PowerMod[10, n! - k!, p], {k, n}], p] > 0 && p < 10000000, p = NextPrime[p]]; p, {n, 2, 24}]
nonn,more
T. D. Noe, Apr 05 2016