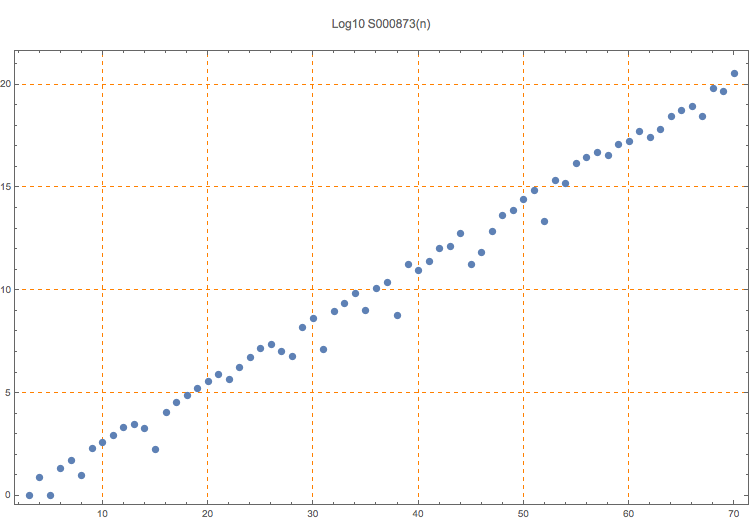
Difference between binomial(2*n,n) and the closest binomial(m,k) with m > 2*n and 1 < k < n-1.
1, 8, 1, 22, 54, 10, 208, 380, 834, 2145, 3041, 1803, 171, 10738, 34183, 75426, 158703, 360825, 758241, 476635, 1707291, 5459286, 14274729, 21782631, 10805516, 6174213, 159670290, 419394696, 13050502, 877612302, 2195995165, 7050787276, 1011881559
3
It is conjectured that the difference is never zero. This would imply that a number does not appear in Pascal’s triangle exactly an odd number (greater than 3) of times. For the terms up to n=70 here, the closest binomial coefficient has the form binomial(m,2). Some of these differences can be seen in the sorted binomials shown in S000874.
T. D. Noe, Plot of terms 3..70
T. D. Noe, Table of terms 3..70
Eric W. Weisstein, MathWorld: Central Binomial Coefficient
Wikipedia, Singmaster’s conjecture
(Mma) Table[targ = Binomial[2*nn, nn]; best = Binomial[2*nn + 1, nn]; nBest = 0; kBest = 0; n = 2*nn + 1; k = nn - 1; While[best > targ && k > 5, While[b = Binomial[n, k]; b < targ, n++]; If[b < best, best = b; nBest = n; kBest = k]; k--]; While[best > targ && k > 1, n = Ceiling[NSolve[Binomial[qq, k] == targ, qq, nn][[-1, 1, 2]]]; b = Binomial[n, k]; If[b < best, best = b; nBest = n; kBest = k]; k--]; best - targ, {nn, 3, 50}]
nonn,hard
T. D. Noe, May 06 2016, May 09 2016