Sorted Diophantine quadruples; s(i)*s(j)+1 is a square for each pair s(i) and s(j), i not equal to j.
1, 3, 8, 120, 2, 4, 12, 420, 1, 8, 15, 528, 3, 5, 16, 1008, 1, 15, 24, 1520, 4, 6, 20, 1980, 3, 8, 21, 2080, 2, 12, 24, 2380, 5, 7, 24, 3432, 1, 24, 35, 3480, 6, 8, 28, 5460, 4, 12, 30, 5852, 3, 16, 33, 6440, 1, 35, 48, 6888, 2, 24, 40, 7812, 7, 9, 32, 8160
1
Each quadruple is sorted and then all quadruples are sorted by the fourth entry. The individual terms are given in the four sequences S000953-S000956. The paper by He Togbe, and Ziegler proved that Diophantine quintuples do not exist.
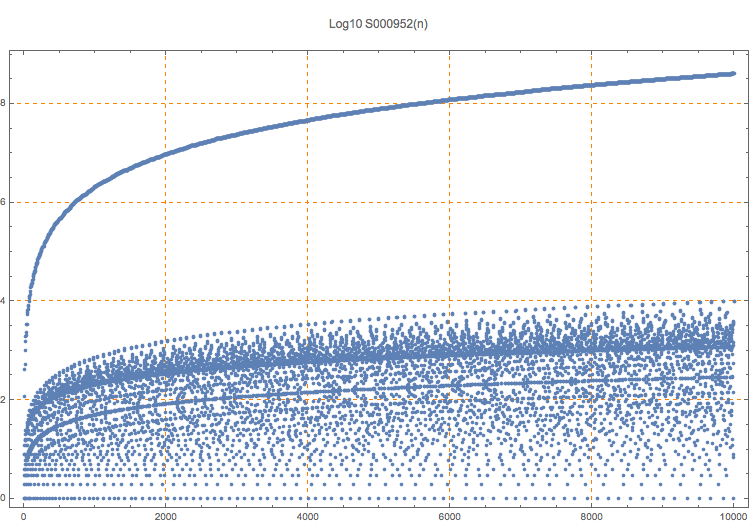
T. D. Noe, Plot of 2500 quadruples
T. D. Noe, Table of 2500 quadruples
Bo He, Alain Togbe, and Volker Ziegler, There is no Diophantine quintuple, arXiv 1610.0402 (Oct 13 2016)
(Mma) nn = 30; t = {}; Do[d = Divisors[k^2 - 1]; p = Take[Transpose[{d, Reverse[d]}], Length[d]/2]; r = Sqrt[1 + Times @@ p[[1]]]; Do[AppendTo[p[[i]], p[[i, 1]] + p[[i, 2]] + 2*r], {i, Length[p]}]; t = Join[t, Table[AppendTo[p[[i]], 4*r*(p[[i, 1]] + r)*(p[[i, 2]] + r)], {i, Length[p]}]], {k, 2, nn}]; t2 = Select[t, #[[4]] <= Transpose[t][[4, -1]] &]; t3 = Sort[t2, #1[[4]] < #2[[4]] &]
nonn,tabl,nice
T. D. Noe, Oct 16 2016