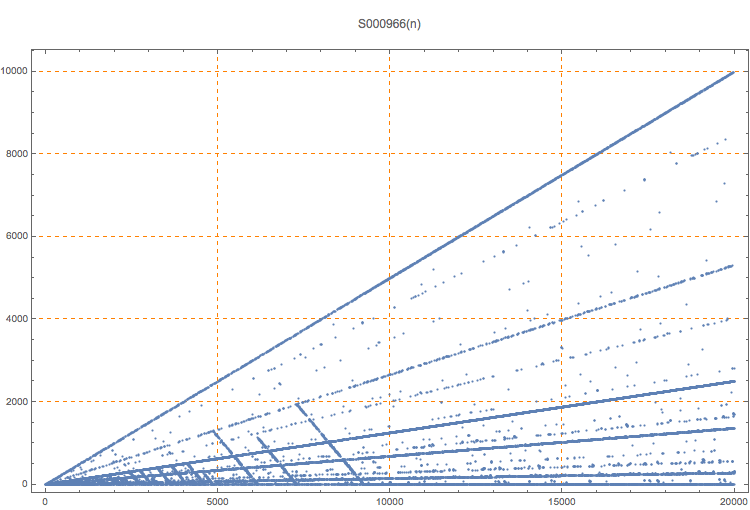
For the Collatz (3x+1) sequence s beginning with n, the difference between n and the next larger number in s, or 0 if there is no larger number.
0, 1, 0, 3, 2, 1, 0, 1, 6, 2, 4, 3, 2, 1, 0, 3, 2, 1, 0, 11, 4, 12, 0, 1, 14, 4, 6, 5, 5, 4, 0, 1, 6, 5, 4, 3, 2, 1, 0, 5, 22, 6, 8, 7, 7, 6, 0, 3, 2, 1, 0, 27, 7, 6, 0, 8, 30, 8, 10, 9, 8, 7, 0, 9, 10, 9, 0, 35, 10, 9, 0, 7, 38, 10, 12, 11, 10, 9, 0, 11, 9, 8
2
In the plot, the diagonal line ending at about 9000 appears to be the last such diagonal. Why?
T. D. Noe, Plot of 20000 terms
T. D. Noe, Table of 20000 terms
(Mma) Collatz[n_] := NestWhileList[If[EvenQ[#], #/2, 3 # + 1] &, n, # > 1 &]; Table[s = Sort[Collatz[n] - n]; ps = Position[s, 0][[1, 1]]; If[Length[s] > ps, s[[ps + 1]], 0], {n, 2, 100}]
Cf. A033496 (n for which there is no larger term), A213330, S000967.
nonn
T. D. Noe, Jan 30 2017