Triples (x,y,z) with 1 < x < y < z and z = y + 2 such that x! y! z! is a square.
2, 7, 9, 3, 23, 25, 4, 23, 25, 7, 34, 36, 2, 48, 50, 10, 62, 64, 6, 79, 81, 5, 119, 121, 8, 124, 126, 9, 124, 126, 11, 174, 176, 18, 219, 221, 3, 241, 243, 4, 241, 243, 2, 287, 289, 26, 321, 323, 14, 350, 352, 17, 934, 936, 6, 1443, 1445, 2, 1680, 1682, 3, 2399, 2401, 4, 2399, 2401, 5, 2644, 2646, 22, 4198, 4200
1
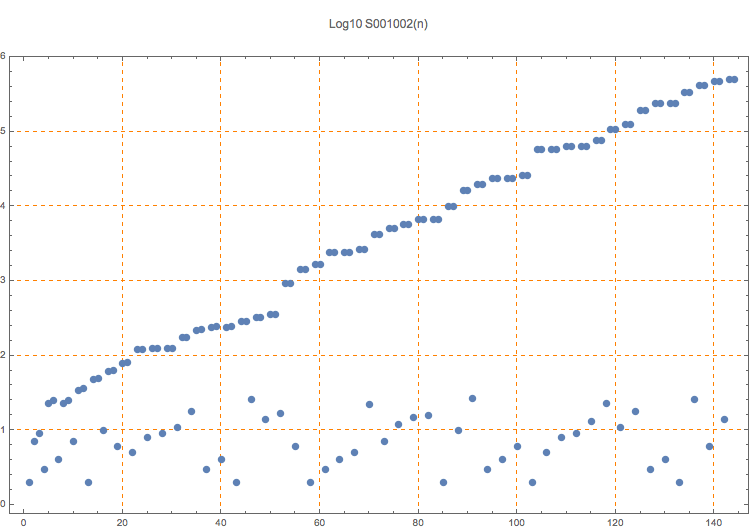
This sequence grows slowly.
T. D. Noe, Plot of 48 triples
T. D. Noe, Table of 48 triples
(Mma) (using the code in S001000) Select[t, #[[3]] - #[[2]] == 2 &]
Cf. S001000.
nonn,tabl
T. D. Noe, Apr 19 2017