Numbers that are not the sum of 17 nonnegative 5-th powers.
18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127
1
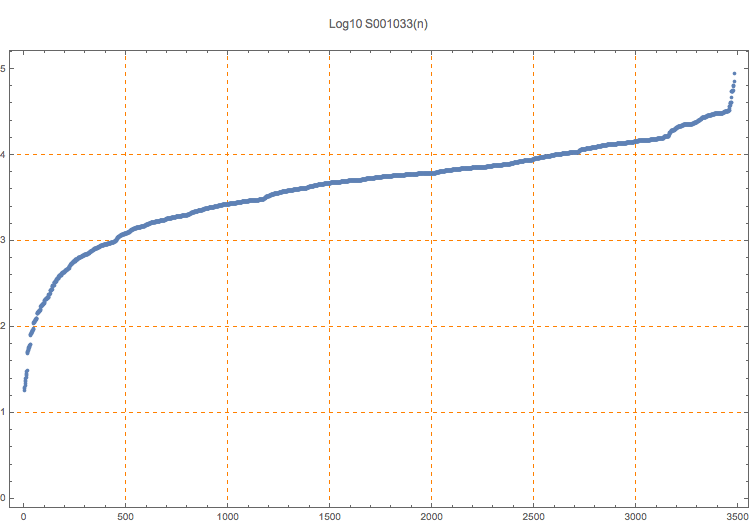
The last number in this sequence appears to be 87918, which means that all numbers greater than 87918 can be written as the sum of 17 nonnegative 5-th powers. Note that the Mathematica program prints only the last 100 terms.
T. D. Noe, Plot of 3481 terms
T. D. Noe, Table of 3481 terms
Wikipedia, Waring’s problem
(Mma) nn = 10; lim = nn^5; t17 = Table[0, {lim}]; Do[num = i^5 + j^5 + k^5 + l^5 + m^5 + n^5 + o^5 + p^5 + q^5 + r^5 + s^5 + t^5 + u^5 + v^5 + w^5 + x^5 + y^5; If[0 < num <= lim, t17[[num]]++], {i, 0, nn}, {j, i, nn}, {k, j, nn}, {l, k, nn}, {m, l, nn}, {n, m, nn}, {o, n, nn}, {p, o, nn}, {q, p, nn}, {r, q, nn}, {s, r, nn}, {t, s, nn}, {u, t, nn}, {v, u, nn}, {w, v, nn}, {x, w, nn}, {y, x, nn}]; Take[Flatten[Position[t17, 0]], -100]
nonn,fini,nice
T. D. Noe, May 23 2017