For each odd prime p, the p least-multiples of p whose prime factors are in arithmetic progression.
3, 15, 105, 5, 35, 935, 21505, 623645, 7, 77, 1729, 177289, 213771607, 33562142299,64260503729605393, 11, 143, 4301, 124729, 423669851, 152542130346128080167261679026481804404220365051, 210818566907450764456549404404027652893181991921
1
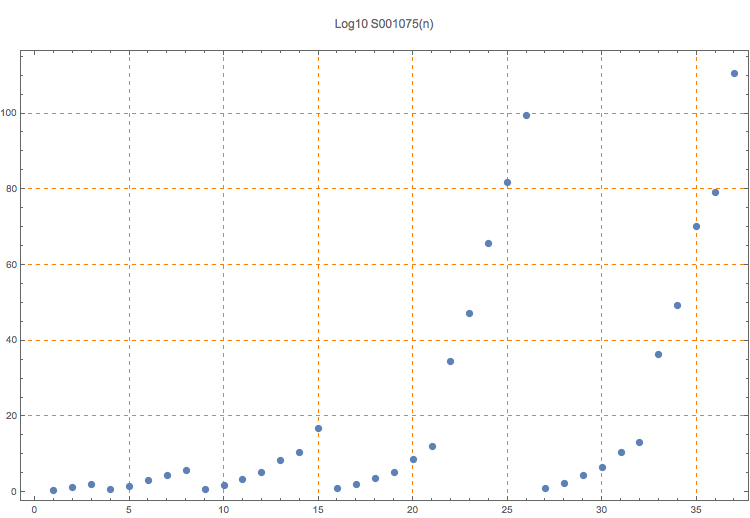
As is evident in the plot, these terms grow very rapidly. The terms for p=13 are incomplete because the numbers are so large; the program ran for over a week to attempt to find the next term. The common difference of the prime factors in given in S001076. An important question is whether such a sequence exists for primes beginning with a given prime p.
T. D. Noe, Plot of 37 terms
T. D. Noe, Table of 37 terms
Example: 623645 = 5 * 11 * 17 * 23 * 29 is the least number whose 5 prime factors begin with 5 and increase linearly.
Wikipedia, Primes in arithmetic progression
(Mma) nn = 4; t = {}; Do[p = Prime[n]; s = {p}; k = 0; While[Length[s] < p, k = k + 2; p2 = p; prod = p; cnt = 1; While[p2 = p2 + k; PrimeQ[p2], cnt++; prod = prod*p2; If[cnt > Length[s], AppendTo[s, prod]]]]; AppendTo[t, s], {n, 2, nn}]; t
Cf. S001076.
nonn,tabf,hard
T. D. Noe, Nov 01 2017