The number n is the first of two consecutive primitive abundant numbers.
82004, 158235, 516704, 2921535, 5801984, 10846016, 12374144, 12603824, 18738224, 24252074, 32409530, 33696975, 35356544, 36149295, 41078114, 42541190, 43485584, 65090864, 88304475, 90725775, 181480695, 183872535, 213261795, 233762528, 242301344
1
A primitive abundant number is an abundant number whose proper divisors are all deficient. These numbers are much less plentiful than the consecutive abundant numbers A096399.
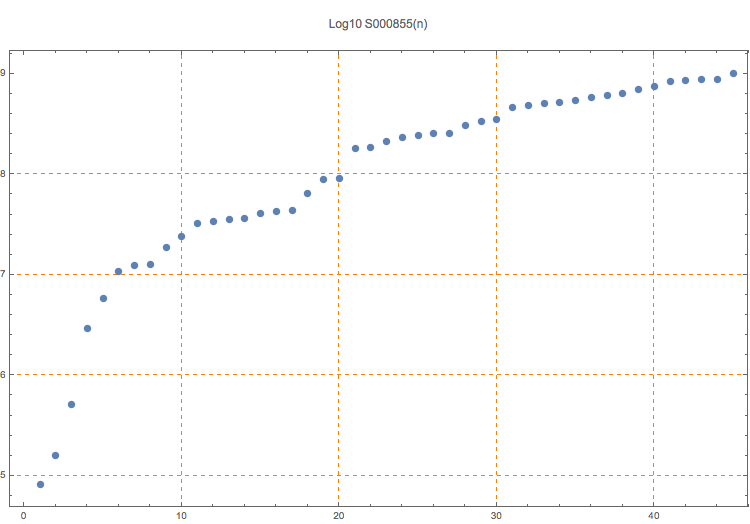
T. D. Noe, Plot of 45 terms
T. D. Noe, Table of 45 terms
Wikipedia, Primitive abundant number
(Mma) abunQ[n_] := DivisorSigma[1, n] >= 2*n; primAbunQ[n_] := Not [Or @@ abunQ /@ Most[Divisors[n]]] && abunQ[n]; nn = 10^7; last = 0; t = Reap[Do[If[DivisorSigma[1, n] >= 2*n, If[last == n - 1, Sow[n - 1]]; last = n], {n, nn}]][[2, 1]]; t2 = Select[t, primAbunQ]; t3 = Select[t + 1, primAbunQ]; t4 = Intersection[t2, t3 - 1]
Cf. A005101 (abundant numbers).
nonn,hard
T. D. Noe, Mar 23 2016