Each row has the n pairs of nonnegative integers whose squares sum to A000446(n).
0, 0, 0, 5, 3, 4, 1, 18, 6, 17, 10, 15, 4, 33, 9, 32, 12, 31, 23, 24, 0, 65, 16, 63, 25, 60, 33, 56, 39, 52, 7, 74, 14, 73, 22, 71, 25, 70, 41, 62, 50, 55, 25, 450, 102, 439, 135, 430, 150, 425, 250, 375, 263, 366, 290, 345, 20, 165, 27, 164, 45, 160, 60, 155, 83, 144, 88, 141, 101, 132, 115, 120
1
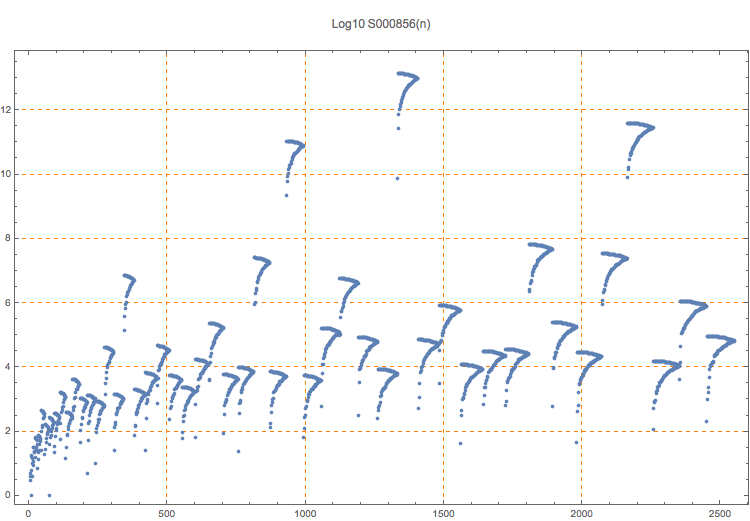
The A000446 sequence has the least squared radius of a circle having n integer points on its circumference in the first quadrant. The n-th row contains 2*n terms. This unusual plot could be called the 7 plot or question-mark plot.
T. D. Noe, Plot of 50 rows
T. D. Noe, Table of 50 rows
(Mma) nn = 50; soln = Table[0, {nn}]; soln[[1]] = {0, {0, 0, 0, 0, 0, 0}}; Do[s1 = Minimize[{5^a 13^b 17^c 29^d 37^e 41^f, 1/2 ((1 + a) (1 + b) (1 + c) (1 + d) (1 + e) (1 + f)) == n, a >= 0, b >= 0, c >= 0, d >= 0, e >= 0, f >= 0}, {a, b, c, d, e, f}, Integers]; s2 = Minimize[{5^a 13^b 17^c 29^d 37^e 41^f, 1/2 (1 + (1 + a) (1 + b) (1 + c) (1 + d) (1 + e) (1 + f)) == n, a >= 0, b >= 0, c >= 0, d >= 0, e >= 0, f >= 0}, {a, b, c, d, e, f}, Integers]; If[s1[[1]] < s2[[1]], soln[[n]] = s1, soln[[n]] = s2]; soln[[n, 2]] = Table[soln[[n, 2]][[i, 2]], {i, 6}]; Print[{n, soln[[n]]}], {n, 2, nn}]; Table[PowersRepresentations[soln[[n]][[1]], 2, 2], {n, nn}]
Cf. A000446.
nonn,tabf
T. D. Noe, Mar 24 2016